Trinomials of the form 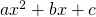 where
where 
A trinomial where ![]() can be difficult to factor. In grade 11 pre-calc, you are required to factor any trinomial of the form
can be difficult to factor. In grade 11 pre-calc, you are required to factor any trinomial of the form ![]() . In grade 10, we need only consider three special cases.
. In grade 10, we need only consider three special cases.
Remember that not all trinomials factor nicely with integers. All the examples here are chosen because they do factor nicely with integers.
Special case 1: No constant term (officially a binomial…).
![]()
The highest common factor of these two terms is ![]() .
.
![Rendered by QuickLaTeX.com \begin{align*}&4x^2-16x\\[10pt]=&4x(x-4)\end{align}](https://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-c29ec98681828286e017636371c9fab2_l3.png)
Special case 2: A common factor between all three terms
![]()
First we notice that 2 divides all three terms. Let’s factor it out:
![Rendered by QuickLaTeX.com \begin{align*}&2x^2-10x+8\\[10pt]=&2(x^2-5x+4)\end{align}](https://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-224a6de4384b048da3b284cf56f33359_l3.png)
The trinomial in the brackets has ![]() and so we can factor by finding two numbers that multiply to 4 and add to
and so we can factor by finding two numbers that multiply to 4 and add to ![]() .
.
![Rendered by QuickLaTeX.com \begin{align*}&2x^2-10x+8\\[10pt]=&2(x^2-5x+4)\\[10pt]=&2(x-4)(x-1)\end{align}](https://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-317b28412f0298952ede4630114d5a97_l3.png)
Special case 3: A difference of two squares (also, officially a binomial, not a trinomial).
![]()
This example follows the format ![]()
In this case, ![]() and
and ![]() . Therefore,
. Therefore,
![Rendered by QuickLaTeX.com \begin{align*}&4x^2-25\\[10pt]=&(2x-5)(2x+5)\end{align}](https://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-0b31ec75058209c751dfbb0aec9f00bf_l3.png)
Practice:
A note on names: A trinomial is a polynomial with three terms. A quadrilateral is a polynomial with degree 2, meaning that the highest power of a term is 2 and it has an ![]() term. Quadrilaterals are often trinomials, but not always.
term. Quadrilaterals are often trinomials, but not always.