We use the word trigonometry to refer to the relationship between the side lengths and angles of a right angle triangle. Trigonometry doesn’t end with right-angled triangles, but its a good place to start.
As we know, a triangle has three sides and three angles. On a right-angled triangle, it is given that one angle is 90°.
Trigonometry uses a set of numbers we refer to as ‘trig values’. The trig values we see on our calculators today come to us after more than 2000 years of math study, translation and collaboration – to make them ever more perfect and useful.
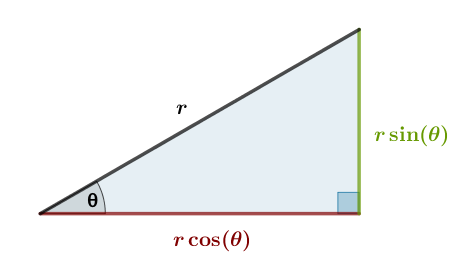
A right triangle with hypotenuse 1 has two trig values: a sine (sin) and a cosine (cos). We use those values to calculate the sides of all other similar triangles.
Until the invention of the scientific calculator in the 1970s, sine and cosine values were recorded in long tables.
Trigonometry: Meter Stick Trig Table
Collaborate as a class to create a trig table, using meter sticks and a print out of angles 5° to 85°. Meter stick Trig Table Angles 5 to 85
Use the applet below to check see how accurate your measurements are.
Triangles that have hypotenuse length 1
On this applet, the hypotenuse has been set to 1.
GeoGebra link to applet, GeoGebra link to interactive lesson
(a) What angle makes the red and green side equal in length?
(b) What angle makes the adjacent side (red) 0.5?
(c) What is the relationship between the lengths of the red side, the green side and the hypotenuse?
(d) What does a very large angle do to the red side?
(e) What does a very large angle do to the green side?
(f) When the angle is 20°, the green side is 0.342; the red side is 0.94. At what angle do they swap, that is, the red is 0.342 and the green is 0.94?
(g) What does Pythagoras’ Theorem say about the length of the red side, the green side and the hypotenuse? Try it out for any angle.
Sines, Cosines, Tangents
The green and red sides of the right-angled triangle hypotenuse 1 are available on any scientific calculator.
On the applet above (hypotenuse 1), change the angle to 24°.
On a scientific calculator, ensure the screen says ‘DEG’ or ‘D’ for degree mode; and type in sin(24°); cos(24°) and tan(24°).
The green length; which is opposite the marked angle; is the sine of the marked angle (rounded to 2 d.p). The red, adjacent length is the cosine.
Every other right-angled triangle with angle 24° is an enlargement of this right-angled triangle.
Suppose we have a right-angled triangle with hypotenuse = 8 and given angle = 24°.
Type in 
and 
on your scientific calculator. Verify your answers with the applet below – change the hypotenuse to 8 and the angle to 24.
In general
On a right angled triangle with hypotenuse length 1, the sine of an angle is the length of the side opposite that angle; the cosine the adjacent; the tangent the division of opposite over adjacent.
For enlargements, the scale factor is the length of the hypotenuse:
Apply
- Open the right angled triangle hypotenuse 1 in a new window.
- Change the angle to match the acute angle given in the triangle below.
- Use the sine – the green side – of the triangle hypotenuse 1.
- Multiply the sine by the length of the hypotenuse. This gives you the length of the opposite side. Enter it to the applet below.
- Do the same for the adjacent (red side). Example of calculation.
The tangent ratio
The tangent is the opposite side divided by the adjacent side (green divided by red). The name of the tangent makes sense when seen on a circle, as it is is a length marked on the tangent of the circle at the angle of reference. This diagram shows that 
.
Let O be the center of the circle. OB is the radius, so OB = 1.
![\[\frac{AB}{OB}=\frac{\text{tan(24°)}}{1}\]](https://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-41b24d4fe96aca4501f6713ec76194f0_l3.png "Rendered by QuickLaTeX.com")
Because triangle OAB is similar to the smaller triangle with hypotenuse 1, we can say that
![\[\frac{AB}{OB}=\frac{\text{green}}{\text{red}}\]](https://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-58882e207cea6c0cff440cdd2de620d2_l3.png "Rendered by QuickLaTeX.com")
Concluding that
![\[\frac{\text{tan(24°)}}{1}=\frac{\text{green}}{\text{red}}\]](https://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-cb0926a78cd7ead9d7e0f52a45bfe7e9_l3.png "Rendered by QuickLaTeX.com")
in other words
![\[tan(24°)=\frac{\text{opp}}{\text{adj}}\]](https://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-b4706d80b8f86221327579d908588bac_l3.png "Rendered by QuickLaTeX.com")
Sines, Cosines and Tangents for any angle
On this page we have defined sine, cosine and tangent for angles between 0 and 90 degrees. However, sine, cosine and tangent values can be measured or calculated for any angle. See Visual Trig Values.
The name ‘tangent’ makes sense as it is a measurement on the tangent of the circle. Where does the name ‘sine’ come from? Read the story of the name ‘sine’ here: https://www2.clarku.edu/faculty/djoyce/trig/chords.html