Three forms of a Quadratic Expression

A quadratic expression has three common presentations.

  1. Standard (or polynomial) form:         ax^2+bx+c
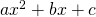
  2. Factored form                                   a(x-r_1)(x-r_2)
  3. Completed square (or vertex) form  a(x-h)^2+k

Let’s see the expression x^2-4x-5 in these three forms:

  1. Standard form is simply     x^2-4x-5
  2. Factored form                    (x-5)(x+1)
  3. Completed square form     (x-2)^2-9

These three forms are equivalent. No matter what value of x you might choose, the three forms will compute to the same value.

Let’s check with x=10

  1. x^2-4x-5\quad =10^2-4(10)-5\quad=100-40-5\quad=55
  2. (x-5)(x+1)\quad=(10-5)(10+1)\quad=5\times 11 \quad =55
  3. (x-2)^2-9\quad =(10-2)^2-9\quad=8^2-9=64-9\quad =55

Now, spot checking like this is not a proof. I could have engineered that 10 would work, yet nothing else does. Beginning with one form, and algebraically changing its form will constitute a proof. We’ll do that work at the end of this page.

Let’s see the graph of this function, f(x)=x^2-4x-5.

Notice that the y intercept (0,-5 )is the constant in the standard form f(x)=x^2-4x-5.

Notice that the x intercepts seem to be related to the factored form, f(x)=(x+1)(x-5).

Notice that the vertex (turning point) seems to be related to the completed square form f(x)=(x-2)^2-9.

In this unit, we find out how to algebraically convert from one form to another, and find out what each form is particularly useful for.

Proof of Equivalence

Show that (x+1)(x-5)=x^2-4x-5

    \begin{align*}\text{left hand side }&=(x+1)(x-5)\hspace{1.5 cm} \text{multiply out brackets}\\[10 pt]&=x^2-5x+x-5 \hspace{1.3 cm} \text{gather like terms}\\[10 pt]&=x^2-4x-5 =\text{ right hand side.}\end{align}

Show that (x-2)^2-9=x^2-4x-5

    \begin{align*}\text{left hand side }&=(x-2)^2-9\\[10 pt]&=(x-2)(x-2)-9 \hspace{1.5 cm} \text{multiply out brackets}\\[10 pt]&=x^2-2x-2x+4-9\hspace{1.1 cm} \text{gather like terms}\\[10 pt]&=x^2-4x-5 = \text{right hand side.}\end{align}

As Euclid postulated a long time ago, things that are equal are equal to each other. So if  (x+1)(x-5)=x^2-4x-5 and (x-2)^2-9=x^2-4x-5 then (x-2)^2-9=(x+1)(x-5)

Therefore all three expressions are equivalent.