When multiplying a binomial (an expression with two terms) by another binomial, we end up with four terms.

Oftentimes, some of the terms can be gathered and so your final expression might have three or even less terms.

Example 1: Integers – a simpler way to multiply

Here’s an example where both terms in both binomials are just integers.

$27 \times 34=(20+7)(30+4)$

Let’s suppose the numbers are actually the length and width of a rectangle.

By letting $27=20+7$ and $34=30+4$ we create four simple calculations.

$\begin{align*}&7 \times 30 = 210\\[10pt]7 \times 4 = 28\\[10pt]20\times 30=600\\[10pt]&20\times 4 = 80\end{align*}$

Therefore the total area of this rectangle, or the answer to $27 \times 34$ is $210+28+600+80$ which is $890+28=918$ .

In other words, $(20+7)(30+4)=600+80+210+28$ . In the examples, we see how to go from the brackets to the four terms without drawing the rectangle.

Example 2: the terms are a, b, c and d

In general, to multiply a binomial by binomial we are multiplying

$(a+b)(c+d)$

Where the $a, b, c$ and $d$ can be any number or variable or mixture of numbers and variables.

Using a rectangle diagram, let the width be $a+b$ units; the length be $c+d$ units.

The total area of the rectangle is $ac+ad+bc+bd$ .

There are no like terms, so this expression can’t be simplified further.

Example 3: The classic

Although the $a, b, c$ and $d$ can be any values, this course is geared towards studying quadratic equations which involve an $x^2$ term.

Most of the expressions from here on look like $(x+4)(x+5)$ . Here is a rectangle model of this expression:

Notice that $(x+4)(x+5)$ can be calculated with four smaller calculations:

$x^2+4x+5x+20$ .

We notice that $4x+5x=9x$

Therefore,

$(x+4)(x+5)=x^2+9x+20$

Example 4: Without drawing the rectangle

Suppose we wish to expand and simplify:

$(x+2)(x+6)$

without drawing the rectangle.

From the rectangle diagrams, we notice that everything in the first bracket multiplies everything in the second bracket. We can write this as follows:

$\begin{align*}&(x+2)(x+6)\\[10pt]=&x(x+6)+2(x+6)\\[10pt]=&x^2+6x+2x+12\\[10pt]=&x^2+8x+12\end{align*}$

Example 5: The algorithm FOIL: First Outside Inside Last

We multiply the first terms in each bracket to get $x^2$

We multiply the outside terms in each bracket to get $6x$

We multiply the inside terms in each bracket to get $2x$

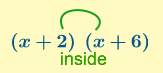
We multiply the last terms in each bracket to get $12$ .

Then we add those terms together and simplify to $x^2+8x+12$ .

Example 6: Watch out!

Remember that a square number means multiply the number by the number? So…

$(x-5)^2$

is expanded as follows:

$\begin{align*}&(x-5)^2\\[10pt]=&(x-5)(x-5)\\[10pt]=&x^2-5x-5x+25\\[10pt]=&x^2-10x+25\end{align*}$

Notice that the answer is not simply $x^2+5^2$ – exponents do not distribute over addition.

Example 7: When the first factor is a whole number:

$\begin{align*}&3(x-10)(2x-1)\\[10pt]=&3(2x^2-x-20x+10)\\[10pt]=&3(2x^2-21x+10)\\[10pt]=&6x^2-63x+30\end{align*}$

alternatively, multiply the three into the first bracket:

$\begin{align*}&3(x-10)(2x-1)\\[10pt]=&(3x-30)(2x-1)\\[10pt]=&6x^2-3x-60x+30=\\[10pt]=&6x^2-63x-30\end{align*}$

Example 8: When the first factor is negative one:

$\begin{align*}&-(x-10)(2x-1)\\=&-(2x^2-x-20x+10)\\[10pt]=&-(2x^2-21x+10)\\[10pt]=&-2x^2+21x-10\end{align*}$

Practice

Use paper and pencil before entering your answer.

Applet link: https://www.geogebra.org/m/udx9xygp

Practice Expanding brackets of all kinds on tranum maths: https://www.transum.org/software/SW/Starter_of_the_day/Students/Brackets.asp?Level=9

Example 9: Extending the principle

In example 4 we said that ‘everything in the first bracket multiplies everything in the second.’

With a little rectangle drawing, we can see how this principle extends to any number of terms in any number of brackets. Let’s expand

$\begin{align*}&(x+y+3)(x+2)\\[10pt]=&x(x+2)+y(x+2)+3(x+2)\\[10pt]=&x^2+2x+yx+2y+3x+6\\[10pt]=&x^2+5x+yx+2y+6\end{align*}$

For three brackets, we simply multiply out the first two then we have two brackets. Etc.

$\begin{align*}&(x+2)(x+3)(x+6)\\[10pt]=&(x^2+3x+2x+6)(x+6)\\[10pt]=&(x^2+5x+6)(x+6)\\[10pt]=&x^2(x+6)+5x(x+6)+6(x+6)\\[10pt]=&x^3+6x^2+5x^2+30x+6x+36\\[10pt]=&x^3+11x^2+36x+36\end{align*}$

Try the ten questions at the bottom of this MathisFun page here.

Top BC G10 Menu Number and Algebra Menu

Interactive Math Resources for Classroom Discussion, Inquiry and Distance Learning

Multiplying Two Binomials

Example 6: Watch out!

Practice