A sequence of polygons
The objective of this project is to create and analyze sequences using GeoGebra and your knowledge of arithmetic sequences.
Project description: Arithmetic Sequences Project tasks
Explore: Use the following instructions to explore various sequence diagrams.
To begin, open a GeoGebra classic page, (close the keyboard) then open a long input bar at the bottom as follows:

For each command given as an example, either type carefully to include all brackets or copy and paste into the input bar on the GeoGebra page.
A Sequence
A sequence until now has simply been a list of numbers. The sequence command in GeoGebra is as follows:

Fill in the input options as follows:

Sequence(2n+1,n,1,10,1)
Press enter, to generate a simple sequence of numbers:

Sequence of points
A point is an ordered pair: it contains an ![]() and a
and a ![]() coordinate. To draw a graph of an arithmetic sequence, we use the
coordinate. To draw a graph of an arithmetic sequence, we use the ![]() values
values ![]() to represent the place in the sequence.
to represent the place in the sequence.
Copy/Type in the sequence command
Sequence((n,2n+1),n,1,10,1)
This generates the set of points
![]()
Sequences of Circles
The circle command requires a point for the center, and a radius.

Example 1. Clear your GeoGebra screen and type in the following set of circles, one at a time:
Circle((1,1),1)
Circle((2,2),1)
Circle((3,3),1)
Circle((4,4),1)
This should give four circles, all with different centers but radius 1.
What they have in common is that the centers are at the point (n,n) between ![]() and
and ![]()
Now, clear the screen and enter all of them together with one sequence command:

Sequence(circle((n,n),1),n,1,4,1)
This means, circle center (n,n) with radius 1, for all values of n between 1 and 4, going up in ones.
Example 2.
Now enter
Sequence(circle((n,n),1),n,1,4,0.1)
Which means, circle center (n,n) with radius 1, for all values of n between 1 and 4, going up in 0.1s – which draws a total of 31 circles!
Example 3. Suppose we make a sequence of circles with center ![]() and with radius
and with radius ![]() .
.
Try out the following command:

Sequence[Circle[(10,5),n],n,1,5]
Example 4. Now let’s add the ‘increment parameter’ and make it 0.1, to draw many more circles.
Sequence[Circle[(10,5), n], n, 1, 5, 0.1]
The final parameter changes the increment of ![]() from the default value 1 to 0.1. More steps between 1 and 5 – more circles.
from the default value 1 to 0.1. More steps between 1 and 5 – more circles.
Make some of your own
- Make a sequence where the center of the circle is constant, but the radius changes.
- Make a sequence where the center of the circle changes, but the radius is constant.
- Make a sequence where the center and the radius both change.
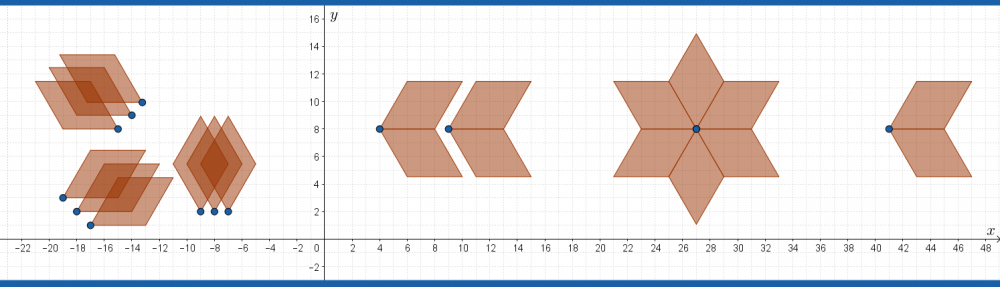
Figure out the sequence command
Now see if you can reproduce the following diagrams:
TUnnel

eye 1

eye 2

Sequences of Line Segments
The following diagram uses the sequence command along with the command Segment[<point>,<point>] to create a sequence of line segments.
Example 1. What will the following command produce? Try it out.

Example 2. Observe the start/end point to a few of line segments to see the pattern of start and end points.

Project outline: