Project: Prime Factors -

Prime factors and fraction arithmetic

The objective of this project is to deepen understanding of integers by using prime factors of integer pairs to simplify fractions, add fractions and to examine the ‘keep change flip’ algorithm for dividing fractions.

You are to complete your own detailed calculations for each operation using (a) an integer pair less than 100, (b) an integer pair greater than 100. Use the applets linked to find a nice set of integer pairs for both parts. Choose good examples.

An example of each operation is written below.

Page Structure:

Title page: title, name, date, objective
Draw a prime factor tree for two integers $m$ , $n$ , both less than 100. Simplify the fraction $\frac{m}{n}$ using the prime factors.
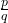Draw a prime factor tree for two new integers $p$ , $q$ , both more than 100. Simplify the fraction $\frac{p}{q}$ using the prime factors.
Add fractions the fractions 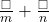$\frac{\square}{m}+\frac{\square}{n}$ , using $m$ , $n$ from page 2, choose your own integers for the numerators.
Add fractions the fractions $\frac{\square}{p}+\frac{\square}{q}$ , using $m$ , $n$ from page 3, choose your own integers for the numerators.
Divide fractions. Create your own example. Show that (explain why, not what) 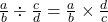$\frac{a}{b}\div\frac{c}{d}=\frac{a}{b}\times\frac{d}{c}$ . Choose your own values for $a, b, c$ and $d$ .
(optional). Divide fractions, generalized. Begin with (where values are not given and not related to previous pages). Or, Square/Cube other roots. Explain how prime factors can identify square roots/cube roots by creating your own examples & generalising.

Learn/review prime factors:

Prime Factors HCM and LCM

Grading

Please refer to the general grading criteria. In addition:

Communication: I have used the correct math vocabulary. For example: factor, prime factor, multiple, least common multiple, greatest common factor, $a$ divides $b$ , meaning $b \div a$ is an integer – this can also be written as $a|b$ .

Reasoning: My writing is sufficient to explain my arithmetic.

Examples

Simplify

We know

$\frac{24}{36}=\frac{2}{3}$

because

$\frac{24}{36}=\frac{24\div12}{36\div12}=\frac{2}{3}$

Let’s break it down with prime factors.

After drawing a prime factor tree for each integer, we calculate that

$\begin{align*}24&=2\cdot 2\cdot 2\cdot 3\\[10pt] 36&=2\cdot 2\cdot 3\cdot 3\end{align*}$

We can write

$\begin{align*}\frac{24}{36}&=\frac{2\cdot 2\cdot 2\cdot 3}{2\cdot 2\cdot 3\cdot 3}\\[10pt] &=\frac{\cancel{2}\cdot \cancel{2}\cdot 2\cdot \cancel{3}}{\cancel{2}\cdot \cancel{2}\cdot \cancel{3}\cdot 3}\\[10pt]&=\frac{2}{3}\end{align*}$

We can express the same calculation using exponents and applying exponent laws:

$\begin{align*}\frac{24}{36}&=\frac{2^3\cdot 3}{2^2\cdot 3^2}\\[10pt] &=\frac{2^3}{2^2}\cdot \frac{3}{3^2}\\[10pt] &=\frac{2}{3}\end{align*}$

Adding

$\frac{7}{24}+\frac{5}{36}$

To add fractions with denominators 24 and 36, we require the lowest common multiple of 24 and 36.

$LCM(24,36) =?$

We require the full set of factors from the larger number, 36:

$36 = 2\cdot 2\cdot 3\cdot 3$

But 36 does not contain all the prime factors of 24, which are 2, 2, 2 and 3. We need another ‘2’.

$LCM(24,36) =(2\cdot 2\cdot 3\cdot 3)\times 2=72$

$\begin{align*}72&=24\times 3\\[10pt] 72&=36\times 2\end{align*}$

Now we can proceed:

$\begin{align*}&\frac{7}{24}+\frac{5}{36}\\[10pt] =&\frac{3}{3}\cdot\frac{7}{24}+\frac{2}{2}\cdot\frac{5}{36}\\[10pt]=&\frac{21}{72}+\frac{10}{72}\\[10pt]=&\frac{31}{72}\end{align*}$

After drawing a prime factor tree for 31 we find that 31 is a prime number and so this final fraction can’t be simplified.

Divide

We know that to multiply fractions we can multiply the numerators and multiply the denominators:

$\frac{6}{7}\times \frac{2}{3}=\frac{6\times 2}{7 \times 3}=\frac{12}{21}$

Division is the reverse process. We can simply divide across the numerator, divide across the denominator.

$\frac{12}{21}\div\frac{2}{3}=\frac{12\div 2}{21 \div 3}=\frac{6}{7}$

We run into problems when the numerator or denominator doesn’t divide nicely:

$\frac{4}{5}\div \frac{3}{7}=\frac{4 \div 3}{5 \div 7}=\dots$

We are generally taught to use ‘keep, change, flip’. Let’s understand why that works using factors and equivalent fractions.

To divide any fraction by $\frac{3}{7}$ we require a numerator that is a multiple of 3, and a denominator that is a multiple of 7.

Let’s use the least common multiple of 3 and 7. $LCM(3,7)=21$ but we will express 21 with the factors 3 and 7.

Make a fraction equivalent to $\frac{4}{5}$ such that the numerator that is a multiple of 3, and a denominator that is a multiple of 7.

$\frac{4}{5}=\frac{4\times 3\times 7}{5\times 3 \times 7}$

There is no need to calculate the new numerator and denominator as we will see:

$\begin{align*}&\frac{4}{5}\div \frac{3}{7}\\[10pt]=&\frac{4\times 3\times 7}{5 \times 3 \times 7}\div \frac{3}{7}\\[10pt]=&\frac{4\times 3\times 7\div 3}{5 \times 3 \times 7\div 7}\\[10pt]=&\frac{4\,\cancel{\times 3}\times 7\,\cancel{\div 3}}{5 \times 3\, \cancel{\times 7\div 7}}\\[10pt]=&\frac{4\times 7}{5 \times 3}\end{align*}$

We can now identify where ‘Keep, Change, Flip’ comes from.

Let’s proceed to the answer:

$\frac{4\times 7}{5 \times 3}=\frac{28}{15}$

Now the final integers 28 and 15 are coprime. That means, although they aren’t prime, they don’t share any factors. The final answer can’t be simplified.