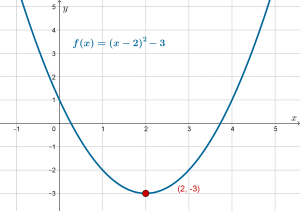
Click new a few times to see how the competed square form of the quadratic expression leads us directly to the coordinates of the vertex.

The completed square form is also known as the vertex form.

How it works

To calculate $x_{v}$ , the $x$ -coordinate of the vertex, we solve $x-2=0$ . This is why:

This parabola has a minimum point. That is, $y$ , or $f(x)$ has a minimum value. The number $y$ is made up of two parts, we need to find the minimum of each part:

$y= \quad \quad(x-2)^2 \quad \quad-3$

The first part of $y$ is $(x-2)^2$ . What is the minimum value of $(x-2)^2$ ? This number is a square number. What is the minimum square number? The minimum square number is $0$ , because $0^2=0$ and there are no negative square numbers.

The second part of the number $y$ is the constant $-3$ . This cannot change.

To find the minimum value of both parts of $y$ we need $x$ such that $(x-2)^2=0$ .

Solve

$\begin{align*}(x-2)^2&=0\\[10 pt]x-2&=0\\[10 pt]x&=2\end{align}$

To calculate $y_{v}$ , the $y$ -coordinate of the vertex, we evaluate the function at $x_{v}$ , which in our case is $x=2$ .

$\begin{align*}f(x)&=(x-2)^2-3\\[10 pt]f(2)&=(2-2)^2-3\\[10 pt]&=-3\end{align}$

In general, if $f(x)=a(x-h)^2+k$ , then $x_{v}=h$ and $y_{v}=k$ .

This is true if the coefficient $a$ is positive or negative.

applet link

Other ways to find the vertex

Factoring

If the parabola factors, we can easily find the roots. $x_{v}$ is half way between the roots, which we can find by $x_{v}=\dfrac{r_1+r_2}{2}$ . We can then find $y_{v}$ by substituting the $x$ value into the equation for $y$ .

Example

$\begin{align*}y&=x^2-2x-8\\[10 pt]\Rightarrow y&=(x-4)(x+2)\\[10 pt]\text{For x-intercepts, }0&=(x-4)(x+2)\\[10 pt]\Rightarrow x&=4 \,\, \text{ or }\,\, x=-2\\[10 pt]\text{For vertex, }x_v&=\dfrac{4+(-2)}{2}=1\\[10 pt]y_v&=(1)^2-2(1)-8=-9\\[10 pt]\text{Vertex is at }&(1,-9)\end{align}$

Formula

We can apply the same process to the roots when they are found using the quadratic formula. The roots are:

$x_1=\dfrac{-b-\sqrt{b^2-4ac}}{2a} \hspace{2 cm}x_2=\dfrac{-b+\sqrt{b^2-4ac}}{2a}$

Adding together gives:

$\begin{align*}&\dfrac{-b-\sqrt{b^2-4ac}}{2a} +\dfrac{-b+\sqrt{b^2-4ac}}{2a}\\[10 pt]=&\dfrac{-b-\sqrt{b^2-4ac}+(-b)+\sqrt{b^2-4ac}}{2a}\\[10 pt]=&\dfrac{-2b}{2a}\\[10 pt]=&\dfrac{-b}{a}\end{align}$

Dividing by two gives:

$x_v=\dfrac{-b}{2a}$

This is a nice, simple formula to use anytime.

Example

$y=3x^2-12x+10$

$x_v=\dfrac{-b}{2a}=\dfrac{-(-12)}{2(3)}=\dfrac{12}{6}=2$

To calculate the $y$ -coordinate:

$y_v=3(2)^2-12(2)+10=12-24+10=-2$

The coordinates of the vertex are $(2,-2)$ .

Completing the square: Alternative approach

Since we know that if $y=a(x-h)^2+k$ , then the vertex has coordinates $(h,k)$ . Now if we already know the coordinates of the vertex, we can complete the square directly.

From the calculations in the example above, we see that $y=3x^2-12x+10$ has vertex at coordinates $(2,-2)$ . That is, $h=2$ and $k=-2$ . Also, the leading coefficient $a=3$ . Therefore

$3x^2-12x+10=3(x-2)^2-2$

Interactive Math Resources for Classroom Discussion, Inquiry and Distance Learning

The vertex

How it works

Other ways to find the vertex

Factoring

Formula

Example

Completing the square: Alternative approach